기하학을 조금 알고 있으면 기하공차를 이해하는데 도움이 된다. 용어와 개념을 간단히 설명한다.
도형
도형은 기하학에서 다루는 객체를 말한다. 도형은 객체 그 자체를 말하거나 그것의 둘레 같은 경계를 말하기도 한다. 예를 들면 삼각형은 속이 꽉 찬 삼각형 자체를 도형이라 하기도 하고, 삼각형의 세 변의 모임을 도형이라고 하기도 한다. 도형은 '눈에 보이는 그림으로 묘사할 수 있는 개체'를 말한다고 생각하면 된다. 보통 경계가 유한한 객체를 도형이라고 부른다.
도형의 기본요소
도형의 기본요소는 점, 선, 면이다.
• 점
0차원에 속하며, 크기라는 개념이 없는 가장 단순한 도형이다. 선이 만나는 교차점을 점으로 정의하기도 한다.
— 선
1차원에 속하며, 여러 개의 점들이 모여 이루어진 도형이다. 선은 그 특성에 따라 다음과 같이 나눌 수 있다.
| 직선 | 곡률이 0인 선 | 직선 (↔︎) | 양방향으로 무한한 선 |
| 반직선 (→) | 한 점에서 한쪽으로 무한히 뻗어나가는 무한한 선 | ||
| 선분 (—) | 직선상의 두 점과 그 사이의 점으로 구성되는 유한한 선 | ||
| 곡선 | 곡률이 0보다 큰 선 | 원뿔곡선 (쌍곡선, 포물선), 타원곡선, 팔자곡선 등 | |
◼︎ 면
2차원에 속하며, 면은 다른 말로 평면도형이라고 한다. 평면도형은 2차원 공간 위에 있는 도형이다. 종이 위에 그릴 수 있는 도형이라고 생각하면 된다. 경계선은 직선 또는 곡선으로 이루어질 수 있다. 다각형(삼각형, 사각형, 오각형, 육각형 등), 원, 부채꼴, 타원 등이 평면도형에 속한다.
도형은 워낙 광범위한 개념이기 때문에 상당히 많은 하위항목을 가지고 있다. 1차원 직선 위에 선분들의 모임도 도형이라고 부를 수 있으며, 실제로 묘사할 수 없는 4차원 이상의 객체도 도형이라고 부른다. 하지만 평면 위에 존재하는 평면도형과 우리가 있는 3차원 공간 안에 존재하는 입체도형을 주로 다룬다. 엄밀하게 따져서 점, 선, 면은 그릴 수 없다. 아무리 작은 점이라도 크기가 있고, 아무리 가는 선이라도 크기, 폭, 두께가 있기 때문이다. 점, 선, 면은 머릿속에만 존재하는 이상적인 것이다.
그래도 점, 선, 면에 대해 계속 논의를 해보자. 점이 모여서 선이 되고, 선이 모여서 면이 되고, 면이 모여서 입체가 된다.

차원에 따른 구분
도형은 차원에 따라 그림과 같이 구분할 수 있다. 점은 0차원 도형이다. 선은 1차원 도형이다. 면은 2차원 도형이다. 입체는 3차원 도형이다.

도형의 예시
2차원 도형은 평면도형으로 3차원 도형은 입체도형으로 부르기도 한다.
| 구분 | 정의 | 예시 |
| 평면도형 (2차원 도형) | 길이와 너비만 존재하는 도형, 평면 상의 도형 | 삼각형, 사각형, 원 |
| 입체도형 (3차원 도형) | 길이, 너비, 높이(또는 깊이)가 존재하여 부피를 가지는 도형 | 정육면체, 원기둥, 구, 각기둥, 각뿔, 원뿔, 반구 |
평면도형은 평면공간(2차원 공간)에 있는 도형이고, 입체도형은 입체공간(3차원 공간)에 있는 도형이다.
그렇다면, 곡선은 1차원 도형일까? 2차원 도형일까?
곡선은 1차원 도형이다. 곡선은 점이 연속적으로 움직인 궤적이고, 방향은 바뀌더라도 여전히 길이만 있는 도형, 즉 1차원이다. 직선이 휘어진 것일 뿐, 두께나 넓이는 없기 때문에 차원이 올라가진 않는다. 원의 둘레, 포물선, 사인곡선, 나선, 베지어 곡선 모두 1차원 곡선이다. 단, 공간의 차원과 곡선의 차원은 다를 수 있다. 2차원 평면 위에 그려진 곡선은 2차원 공간 속의 1차원 도형, 3차원 공간 속에 휘도는 곡선은 3차원 공간 속의 1차원 도형이다.
도형은 공간에 있고, 도형은 이론적으로 n차원 공간에 있을 수 있지만 물리적으로 존재하는 3차원까지만 살펴본다.
도형의 자유도
도형이 3차원 공간에 놓이면 자유도가 생긴다. 3차원 공간은 병진자유도 3개와 회전자유도 3개를 제공하지만 도형에 따라 가능한 자유도가 달라진다. 각 도형이 크기가 유한할 때 각 차원의 도형이 가지는 자유도는 어떻게 달라지는지 살펴보자. 참고로 점은 크기를 가지지 않기 때문에 엄밀하게 유한이란 개념이 존재하지 않는다. 또한 입체는 3차원 공간 상에서 경계가 존재하기 때문에 무한이란 개념이 존재하지 않는다.
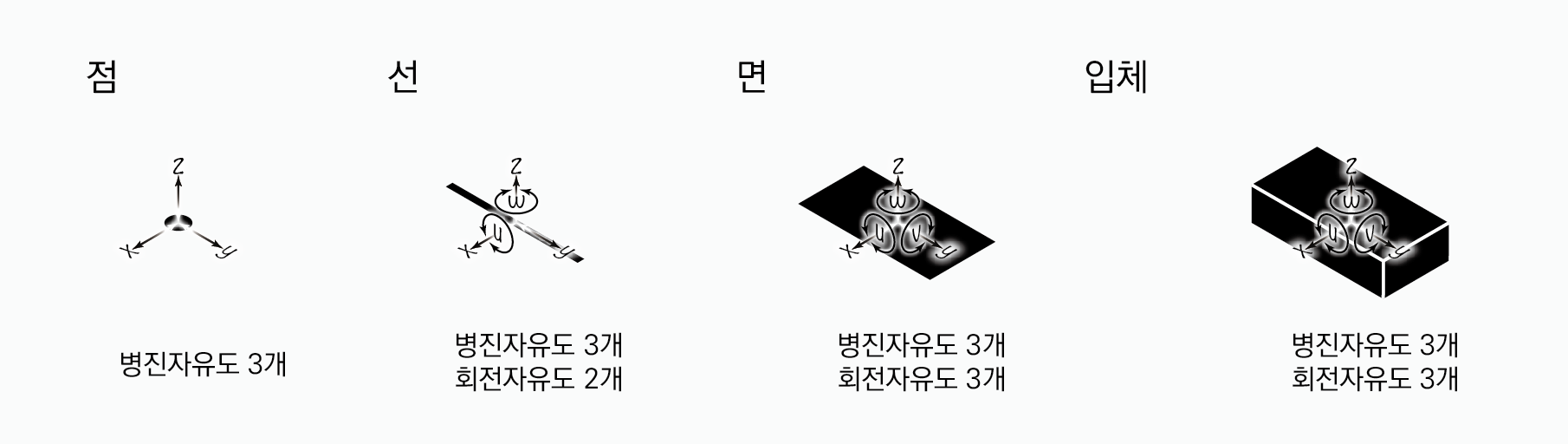
점은 크기가 없기 때문에 회전이 의미가 없다. 따라서 점은 3차원 공간이 제공하는 6개의 자유도 중에서 회전자유도 3개는 의미가 없다. 결과적으로 병진자유도 3개만 생긴다. 선은 선을 중심으로 하는 회전은 의미가 없다. 따라서 3차원 공간이 제공하는 6개의 자유도 중 회전자유도 1개는 의미가 없다. 결과적으로 병진자유도 3개와 회전자유도 2개만 생긴다. 면과 입체는 3차원 공간이 제공하는 6개의 자유도가 모두 생긴다.
공간
앞서 도형이 3차원 공간에 있을 때 생기는 자유도를 살펴보았다. 하지만 도형이 다른 차원에 있다면, 그 차원이 제공하는 자유도로 제한되기 때문에 생기는 자유도가 달라진다.
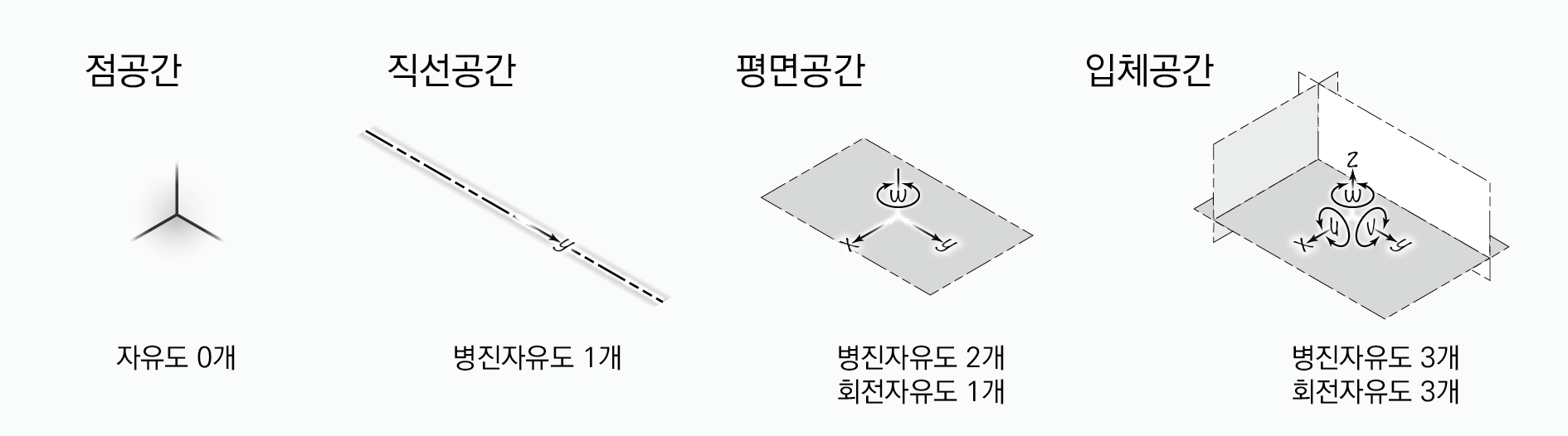
점공간은 0차원 공간이고, 직선공간은 1차원 공간이다. 평면공간은 2차원 공간이다. 입체공간은 3차원 공간이다.

각 차원 공간에서 가능한 자유도는 다음과 같다. 0차원 공간인 점공간은 자유도를 제공하지 않는다. 1차원 공간인 직선공간은 무한한 직선공간이다. 직선공간은 직선을 따라 이동할 수 있는 병진자유도 1개를 제공한다. 2차원 공간인 평면공간은 무한한 평면공간이다. 평면공간은 평면상에서 이동할 수 있는 병진자유도 2개와 회전자유도 1개를 제공한다. 3차원 공간인 입체공간은 무한한 입체공간이다. 입체공간은 평면공간이 3개 합쳐진 것이다. 단순히 산술적으로 보자면 병진자유도 6개와 회전자유도 3개가 있어야 하지만 병진자유도 6개 중 3개가 중복되므로 최종적으로 병진자유도 3개와 회전자유도 3개를 제공한다.
도형과 공간의 관계
각 차원의 도형이 각 차원의 공간에 있을 때 자유도가 어떻게 생성되는지 살펴보자.
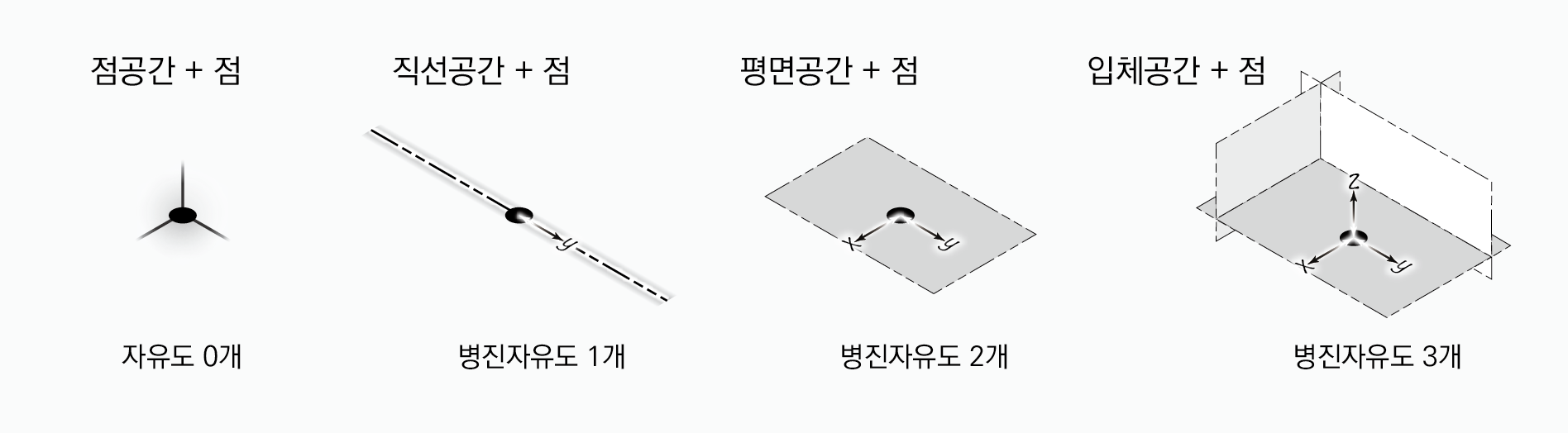
점은 3개의 병진자유도만을 가진다. 그러한 점이 점공간에 있다면, 점은 움직일 수 없다. 따라서 자유도는 0개이다. 점이 직선공간에 있다면, 점은 직선을 따라 한 방향으로만 움직일 수 있다. 따라서 병진자유도 1개가 있다. 점이 평면공간에 있다면, 점은 평면상에서 두 방향으로 움직일 수 있다. 따라서 병진자유도 2개가 있다. 점이 입체공간에 있다면, 점은 입체공간에서 세 방향으로 움직일 수 있다. 따라서 병진자유도 3개가 있다.

도형은 자신의 차원보다 낮은 차원의 공간에 있을 수 없다. 따라서 선은 점공간에 존재할 수 없다. 선은 3개의 병진자유도와 2개의 회전자유도를 가진다. 그러한 선이 직선공간에 있다면, 선은 직선을 따라 한 방향으로만 평행이동할 수 있다. 따라서 병진자유도 1개만 생긴다. 선이 평면공간에 있다면, 선은 평면공간에서 두 방향으로 평행이동할 수 있고, 한 방향으로 회전이동할 수 있다. 따라서 병진자유도 2개와 회전자유도 1개가 생긴다. 선이 입체공간에 있다면, 선은 입체공간에서 세 방향으로 평행이동할 수 있고, 세 방향으로 회전이동할 수 있다. 따라서 병진자유도 3개와 회전자유도 3개가 생긴다.
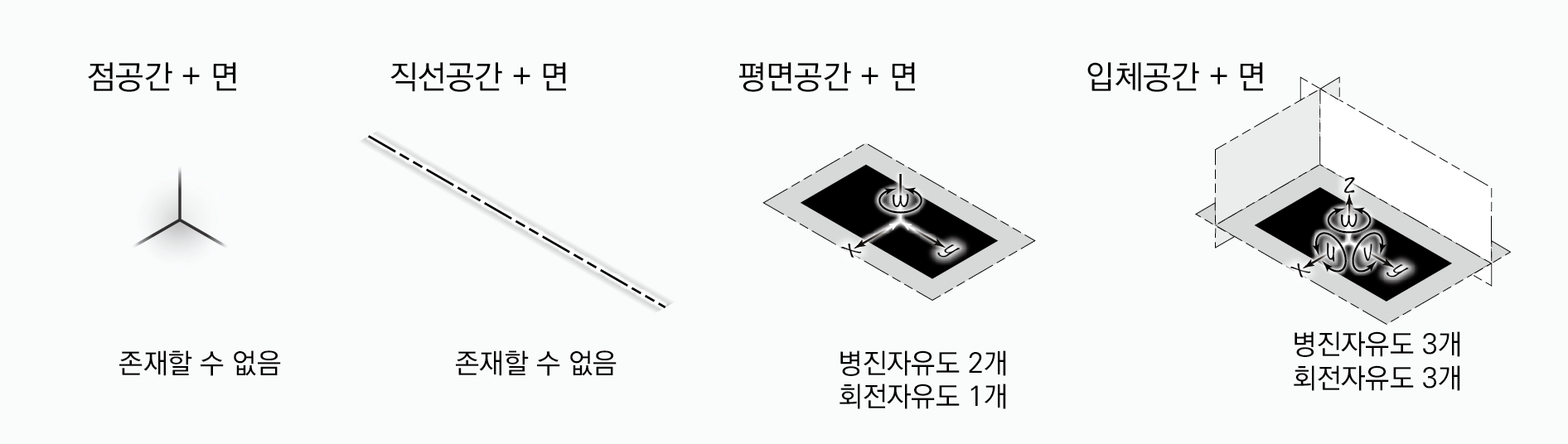
도형은 자신의 차원보다 낮은 차원의 공간에 있을 수 없다. 따라서 면은 점공간, 직선공간에 있을 수 없다. 면은 3개의 병진자유도와 3개의 회전자유도를 가진다. 면이 평면공간에 있다면,면공간에서 두 방향으로 평행이동할 수 있고, 한 방향으로 회전이동할 수 있다. 따라서 병진자유도 2개와 회전자유도 1개가 생긴다. 면이 입체공간에 있다면, 면은 입체공간에서 세 방향으로 평행이동할 수 있고, 세 방향으로 회전이동할 수 있다. 따라서 병진자유도 3개와 회전자유도 3개가 생긴다.

도형은 자신의 차원보다 낮은 차원의 공간에 있을 수 없다. 따라서 면은 점공간, 직선공간, 평면공간에 있을 수 없다. 입체는 3개의 병진자유도와 3개의 회전자유도를 가진다. 입체가 입체공간에 있다면, 입체는 입체공간에서 세 방향으로 평행이동할 수 있고, 세 방향으로 회전이동할 수 있다. 따라서 병진자유도 3개와 회전자유도 3개가 생긴다.
이를 표로 정리하면 다음과 같다.
| 도형과 공간 | 점 | 선 | 면 | 입체 | |
| 병진자유도 3개 | 병진자유도 3개 회전자유도 2개 |
병진자유도 3개 회전자유도 3개 |
병진자유도 3개 회전자유도 3개 |
||
| 점공간 | 자유도 0개 | 자유도 0개 | 존재할 수 없음 | 존재할 수 없음 | 존재할 수 없음 |
| 직선공간 | 병진자유도 1개 | 병진자유도 1개 | 병진자유도 1개 | 존재할 수 없음 | 존재할 수 없음 |
| 평면공간 | 병진자유도 2개 회전자유도 1개 |
병진자유도 2개 | 병진자유도 2개 회전자유도 1개 |
병진자유도 2개 회전자유도 1개 |
존재할 수 없음 |
| 입체공간 | 병진자유도 3개 회전자유도 3개 |
병진자유도 3개 | 병진자유도 3개 회전자유도 2개 |
병진자유도 3개 회전자유도 3개 |
병진자유도 3개 회전자유도 3개 |
도형이 공간에 놓일 때 도형이 가질 수 있는 자유도는 공간이 제공할 수 있는 자유도에 의해 제한된다. 따라서 점공간은 자유도 0개, 직선공간은 병진자유도 1개, 평면공간은 병진자유도 2개와 회전자유도 1개, 입체공간은 병진자유도 3개와 회전자유도 3개를 제공하기 때문에, 해당 차원의 공간에서 도형은 공간이 제공하는 자유도까지만 자유도를 가질 수 있다.
도형이 가질 수 있는 자유도와 공간이 제공할 수 있는 자유도의 이해가 중요한 이유는 DRF의 자유도 개념과 연결되기 때문이다. 이후에 자세하게 설명할 테지만 기본적으로 공차영역은 3차원 입체도형이다. 공차영역이 입체공간에 놓이면 병진자유도 3개와 회전자유도 3개가 생긴다. 하지만 공차영역을 정의하는 FCF에서 데이텀 피쳐를 참조하면, 데이텀 피쳐에 의해 공차영역의 자유도가 제한된다.
간단하게 설명하면, 평면서피스 하나를 데이텀 피쳐로 참조하면, 공차영역이 있는 공간은 6개의 자유도 중 병진자유도 1개와 회전자유도 2개가 제한된다. 따라서 공차영역은 병진자유도 2개와 회전자유도 1개만 생긴다. 평면서피스를 하나 더 데이텀 피쳐로 참조하면, 공차영역이 있는 공간은 병진자유도 2개와 회전자유도 1개가 더 제한된다. 추가로 제한되는 병진자유도 1개는 앞서 제한된 병진자유도 1개와 중복되기 때문에 결과적으로 병진자유도 1개와 회전자유도 1개가 더 제한되어, 결과적으로 병진자유도 2개와 회전자유도 2개가 제한된다.

'기하공차 기초' 카테고리의 다른 글
| 기초 #12 기하공차는 12종류가 5분류로 나누어진다. (5) | 2024.11.12 |
|---|---|
| 기초 #11 기하공차는 무엇을 통제하는가? (1) | 2024.11.12 |
| 기초 #09 피쳐의 종류와 분류 (2) | 2024.11.12 |
| 기초 #08 Rule #1 : ASME Y14.5에서 가장 중요하고 기본이 되는 원칙 (2) | 2024.11.12 |
| 기초 #07 사이즈 피쳐를 사이즈 피쳐답게 하는 경계 (0) | 2024.11.12 |




